
문제 링크 : https://www.acmicpc.net/problem/2579
2579번: 계단 오르기
계단 오르기 게임은 계단 아래 시작점부터 계단 꼭대기에 위치한 도착점까지 가는 게임이다. <그림 1>과 같이 각각의 계단에는 일정한 점수가 쓰여 있는데 계단을 밟으면 그 계단에 쓰여 있는 점
www.acmicpc.net
문제
계단 오르기 게임은 계단 아래 시작점부터 계단 꼭대기에 위치한 도착점까지 가는 게임이다. <그림 1>과 같이 각각의 계단에는 일정한 점수가 쓰여 있는데 계단을 밟으면 그 계단에 쓰여 있는 점수를 얻게 된다.

예를 들어 <그림 2>와 같이 시작점에서부터 첫 번째, 두 번째, 네 번째, 여섯 번째 계단을 밟아 도착점에 도달하면 총 점수는 10 + 20 + 25 + 20 = 75점이 된다.

계단 오르는 데는 다음과 같은 규칙이 있다.
- 계단은 한 번에 한 계단씩 또는 두 계단씩 오를 수 있다. 즉, 한 계단을 밟으면서 이어서 다음 계단이나, 다음 다음 계단으로 오를 수 있다.
- 연속된 세 개의 계단을 모두 밟아서는 안 된다. 단, 시작점은 계단에 포함되지 않는다.
- 마지막 도착 계단은 반드시 밟아야 한다.
따라서 첫 번째 계단을 밟고 이어 두 번째 계단이나, 세 번째 계단으로 오를 수 있다. 하지만, 첫 번째 계단을 밟고 이어 네 번째 계단으로 올라가거나, 첫 번째, 두 번째, 세 번째 계단을 연속해서 모두 밟을 수는 없다.
각 계단에 쓰여 있는 점수가 주어질 때 이 게임에서 얻을 수 있는 총 점수의 최댓값을 구하는 프로그램을 작성하시오.
입력
입력의 첫째 줄에 계단의 개수가 주어진다.
둘째 줄부터 한 줄에 하나씩 제일 아래에 놓인 계단부터 순서대로 각 계단에 쓰여 있는 점수가 주어진다. 계단의 개수는 300이하의 자연수이고, 계단에 쓰여 있는 점수는 10,000이하의 자연수이다.
출력
첫째 줄에 계단 오르기 게임에서 얻을 수 있는 총 점수의 최댓값을 출력한다.
접근방식
문제를 풀고 나서 보니, 전형적인 dp문제였다.
어떻게 접근해야 할지 몰라서 일단은 순차적으로 써봤다.
예를 들어서 계단이 6개이고, 순서대로 계단의 점수가 10, 20, 15, 25, 10, 20 이라고 하자.
계단은 위의 규칙대로, 한 칸씩 오르거나 두 칸씩 올라갈 수 있고, 연속된 세 개의 계단은 오를 수 없다.
dp배열에는 각 계단까지 올라가는 총 점수의 최댓값을 저장
계단 한칸을 오르는 경우의 수)
10
dp상태 : dp[10]

계단 두칸을 오르는 경우의 수)
1. 계단 한칸씩 오르는 경우 : 10 + 20 = 30
2. 계단을 두칸 오르는 경우 : 20
두가지 경우가 있는데, 둘 중 높은 걸 선택해서 dp에 값을 저장
dp상태 : dp[10, 30]

계단 세칸을 오르는 경우의 수)
1. 한칸을 오르고 두칸을 가는 경우 : 10 + 15 = 25
2. 두칸을 오르고 한칸을 가는 경우 : 20 + 15 = 35
2번째의 경우의 점수가 높으므로 35를 dp에 저장
dp상태 : dp[10, 30, 35]

계단 네칸을 오르는 경우의 수)
1. 한칸 -> 한칸 -> 두칸 : 10 + 20 + 25 = 55
2. 한칸 -> 두칸-> 한칸 : 10 + 15 + 25 = 50
1번째 경우의 점수가 높으므로 55를 dp에 저장
dp상태 : dp[10, 30, 35, 55]
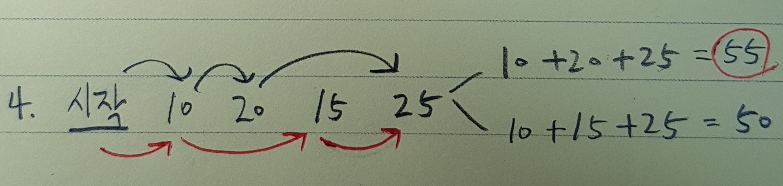
계단 4개의 경우까지 세봤는데, 뭔가 규칙이 보이기 시작한다.
계단을 아래에서 위로 올라가는게 아니라 위에서 아래로 내려간다고 생각해보자.
마지막 계단은 무조건 밟아야 하기 때문에, 역순으로 생각해보자.
위의 사진 기준으로 일단은 25에서 부터 시작하는 곳 까지 가야한다.
2가지 선택지가 존재한다. 한칸을 내려가는 경우와 두칸을 내려가는 경우..
a) 한칸을 내려가는 경우는 25 -> 15
b) 두칸을 내려가는 경우는 25 -> 20
여기에서 선택지가 갈린다.
a) 의 경우에는 연속해서 세칸을 갈 수는 없기 때문에, 25 -> 15 -> 20 순서로는 갈 수 없다. 무조건 15에서 10으로 두칸을 뛰어야 한다. 25 -> 15 -> 10으로 뛴 경우 10에서는 뛰는것에 제한이 없다. 한칸을 뛸 수도 있고 두칸을 뛸 수 도 있다.
물론 저 위의 그림상으로 10은 시작점 바로 윗 칸이므로 한칸밖에 못 가지만, 아래에 계단이 더 있다고 생각을 한다면, 2가지 선택지가 존재 한다.

b) 의 경우에는 2칸을 뛰었기 때문에, 그 다음 계단을 한칸을 내려갈지 두칸을 내려갈지 선택에 아무런 제약이 없다.
25 -> 20으로 뛴 경우, 20까지 올라올 수 있는 최댓값을 더하기만 하면 된다.
그 최댓값은 아래의 계단까지 올라오기까지의 최댓값은 dp에 저장되어 있다.

n개의 계단에 대한 점수가 Stair라는 배열에 저장되어 있다고 하자.
편의상 계단과 dp의 배열 인덱스는 1부터 세는 걸로 하겠다.
n개의 계단을 오르는 경우의 수)
1. 마지막 계단에서 한칸 내려가는 경우
step1 = Stair[n] + Stair[n - 1] + dp[n - 3]
2.마지막 계단에서 두칸을 내려가는 경우
step2 = Stair[n] + dp[n - 2]
step1와 step2 중에 더 큰 값을 선택해서 dp에 저장하면 된다. 식으로 나타내 보면,
dp[n] = Max(step1, step2)
코드로 표현하기만 하면 끝이다.
코드
#include<cstdio>
#include<cstdlib>
int dp[301] = { 0, };
int Max(int a, int b)
{
return a > b ? a : b;
}
int main()
{
int n;
//step1 : jump 한 칸, step2 : jump 두 칸
int step1, step2;
scanf("%d", &n);
int* arr = (int*)malloc(sizeof(int) * (n+1));
for (int i = 1; i <= n; i++) {
scanf("%d", arr + i);
}
dp[1] = arr[1];
dp[2] = arr[1] + arr[2];
step1 = arr[3] + arr[2];
step2 = arr[3] + arr[1];
dp[3] = Max(step1, step2);
for (int i = 4; i <= n; i++) {
step1 = arr[i] + arr[i - 1] + dp[i - 3];
step2 = arr[i] + dp[i - 2];
dp[i] = Max(step1, step2);
}
printf("%d\n", dp[n]);
free(arr);
return 0;
}

위의 설명에 대한 질문이나 틀린 점 있으면 언제든지 댓글로 남겨주세요!
다른 문제의 코드 : https://github.com/DaeeYong/Algorithm-Solution-
DaeeYong/Algorithm-Solution-
Solution for Algorithm Problem. Contribute to DaeeYong/Algorithm-Solution- development by creating an account on GitHub.
github.com
'알고리즘 > 백준 문제풀이' 카테고리의 다른 글
| [C/C++]백준 1992번 - 쿼드트리 (0) | 2021.09.22 |
|---|---|
| [C/C++]백준 2503번 - 숫자야구 (0) | 2021.09.01 |
| [C/C++]백준9095번 - 1,2,3 더하기 (0) | 2021.08.01 |
| [C/C++]백준 1003번 - 피보나치 함수 (0) | 2021.07.29 |
| [C/C++] 백준 1463번 - 1로 만들기 (0) | 2021.07.28 |
