기하학적 변환(geometric Transformations)
이번 내용은 그래픽스에 있어서 엄청나게 중요합니다.
이번 내용을 알게 된다면, 많은 것들을 할 수 있습니다.
여러분들에게 날개를 달아줄 것입니다.

자 그럼 시작해 봅시다.ㅎㅎ
변환에 대해서 이야기해봅시다.
변환이란 무엇일까요?
변환(Transformations)
:물체를 화면상에서 어디에 보여줄 건지에 대한 문제, 실제 화면상에 배치하는 문제
라고 할 수 있습니다.
즉, 다시 말해서
어떤 만들어진 물체의 위치를 바꾸거나, 방향을 바꾸거나, 종횡비를 바꾸는 문제입니다.
임의의 어떤 물체의 크기나, 위치를 바꿔야 할 때 어떻게 바꿀 수 있을지에 대해서 이야기해 볼 예정입니다.
아래는 변환의 예시 이미지입니다.

왼쪽의 이미지는, 사각형의 크기를 늘이고, 줄이고 있습니다.
어떤 형태를 늘이고, 줄이는 것은 기존의 만들어진 물체의 형태 변환하는 것입니다. 너무 당연한 말인가요? ㅎㅎ

다음 이미지는 좌표평면에 있는 물체의 위치가 달라지고 있습니다.
위의 문제들을 어떻게 수학적으로 표현할 수 있을지 설명해보겠습니다.
이제부터 약간의 간단한 수학적인 지식이 필요합니다.
행렬을 도구로 활용할 예정입니다.
변환의 종류에 대해서 생각을 해보면,
1. 회전(Rotation)
2. 확대 및 축소(Scaling)
3. 평행이동(Translation)
으로 나눌 수 있습니다.
여기 있는 3가지만으로도 엄청나게 많은 것들을 할 수 있습니다.
간단한 것부터 시작해봅시다.

위의 그림을 보면 정사각형을 축소시켜서 사각형을 이루는 점들의 좌표가 달라졌습니다.
오른쪽 상단의 꼭짓점의 좌표를 기준으로 한번 생각해봅시다.
(x , y)의 좌표가 새로운 (x’, y’) 좌표로 달라졌습니다.
상단의 꼭짓점을 기준으로 말하자면, (5,5)에서 (2,2)로 좌표가 달라졌습니다.
X와 y의 좌표의 변환을 수식으로 나타내면, 다음과 같습니다.

위의 수식에 (5,5)를 대입하면, x’=2, y’=2 가 나오는 것을 확인할 수 있습니다.
그런데 위와 같이 계속 표기를 하려니 좀 번거롭습니다.
따라서 행렬로 한번 표현해 보려고 합니다.
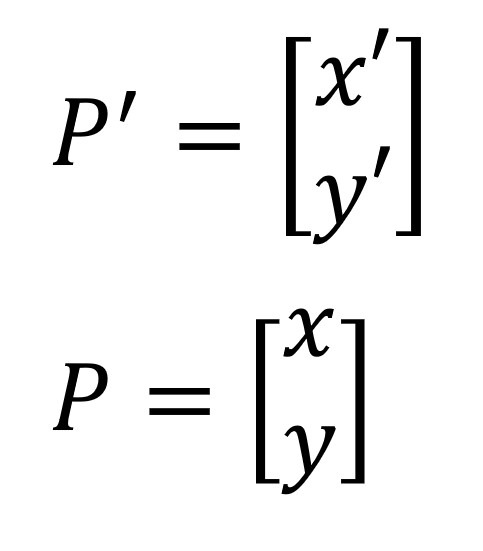
따라서 위의 두 개를 합쳐서 다음과 같이 표현할 수 있습니다.

위의 두 줄의 식이 하나의 식으로 간단하게 표현됩니다.
지금까지 설명한 예제가 Scaling의 예시입니다.
행렬로 표현했을 때의 장점은 하나의 형식으로 여러 가지를 표현할 수 있습니다.
Y=Mx라는 식이 있다고 생각해봅시다. 여기서 M은 행렬입니다.
X에 어떤 좌표를 대입하니, 행렬 계산(M과의 연산)을 거쳐서 새로운 좌표 Y를 얻을 수 있습니다.
기본적인 개념은 어떤 좌표 a가 어떤 행렬과의 연산을 통해서 새로운 좌표 b를 얻는다는 것입니다.
다음 내용부터는 본격적인 translation, rotation, scaling에 대해서 알아보겠습니다.
'컴퓨터 > 컴퓨터그래픽스' 카테고리의 다른 글
| 2-1.그래픽 시스템과 API(graphic system and API) (0) | 2021.02.03 |
|---|---|
| 1-2.컴퓨터 그래픽스란 무엇인가(Introduction) (0) | 2021.01.09 |
| 1-1.컴퓨터 그래픽스란 무엇인가(Introduction) (0) | 2021.01.01 |
| 컴퓨터 그래픽스 소개글 (0) | 2021.01.01 |
| opengl 기본 함수 정리 및 실행화면 (0) | 2020.10.23 |
